In het kort:
Lineaire vervorming betreft afwijkingen in de amplitude en fase van signalen. Deze worden hier behandeld.
Niet-lineaire vervorming betreft het ontstaan van harmonischen en intermodulatie door lineariteitsfouten in de overdracht. Alle componenten in een versterker zijn min-of-meer niet-lineair en kunnen zulke vervorming opleveren. Bij een goed versterkerontwerp -en dat zijn de meeste- is de vervorming uiterst gering..
Verwante onderwerpen:
audio spectrum
vervorming bij: transistoren, elektronenbuizen, zelfinducties, transformatoren
Uitwerken: aanschouwelijk model voor niet-lineaire overdracht.
formule voor kwadratische overdracht.
Hoe ontstaat niet-lineaire vervorming
In alle elektronische
schakelingen ontstaat er in meerdere of mindere mate vervorming van het signaal.
We onderscheiden de lineaire- en de niet-lineaire vervorming. Deze
termen zijn historisch gegroeid en een beetje ongelukkig gekozen.
Bij lineaire
vervorming worden de verschillende frequenties in het audio signaal niet
even sterk doorgegeven en/of treden er fase-verschuivingen (tijdvertragingen)
op. Zulke vervormingen kunnen leiden tot boembassen of juist te weinig laag,
kleuring van het geluid en te weinig of teveel hoge tonen. De elektronische
apparatuur kan gemakkelijk zo gemaakt worden dat zulke vervorming niet optreedt,
zij het dat heel wat versterkers de mogelijkheid bieden om juist aanzienlijke
lineaire vervorming aan te brengen. Dit is de "klankregeling". Meestal
1 knop voor laag en 1 voor het hoog, soms een heleboel knoppen, dan noemen we
het een graphic equalizer.
Luidsprekers zijn de grootste bron van lineaire vervorming, want zelfs de beste
luidsprekers vertonen schommelingen van tientallen procenten in de frequentie
karateristiek. Je bergijpt gelijk dat lineaire vervorming niet gauw als
hinderlijk ervaren wordt.
Bij niet lineaire vervorming ontstaan er frequenties (tonen) die in het oorspronkelijke signaal niet aanwezig waren. Dergelijke vervorming wordt al heel snel als hinderlijk ervaren en het is ook veel moeilijker om zulke vervorming voldoende laag te houden. Percentages van enkele procenten zijn onacceptabel, we streven naar ruim minder dan 1 promille.
De belangrijkste vervormings bron is doorgaans de eindversterker die het vermogen aan de luidprekers levert, alhoewel de luidsprekers zelf ook wel zulke vervorming produceren.
Bij een versterker wordt deze vervoming meestal opgegeven als THD, voor Total Harmonic Distorsion. Bij luidsprekers wordt deze vervorming zelden opgegeven.
In dit hoofdstuk gaat het uitsluitend over de niet-lineaire vervorming.
Hoe ontstaat niet-lineaire vervoming
Bij een ideale versterker is het uitgangs signaal gelijkvormig aan het ingangssignaal, alleen groter. Het ingangssignaal wordt "gespiegeld" via de overdrachts functie, (eng: transfer function) van de versterker. Als die functie (ook wel werklijn genoemd) recht is, zoals hieronder in fig 1, is het uitgangs signaal een duplicaat van het ingangs signaal. De versterking is de helling van die werklijn. In het voorbeeld hier heeft die lijn een helling van 45 graden. Hoe steiler die werklijn, hoe meer versterking. Ik heb de tekeningen in deze voorbeelden gemaakt voor een versterking van 1x omdat ze anders zo groot worden.
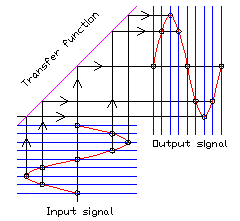
Fig 1. Rechte werklijn. Geen niet-lineaire vervorming.
In fig 2 zie je wat er gebeurt als de werklijn niet recht is. Het ene deel van het signaal wordt meer versterkt dan het andere. Bij een zuiver sinusvormig ingangs signaal is het uitgangs signaal niet meer sinusvormig. En iedere niet sinus-vormige golfvorm bestaat uit een optelling van sinusen met de grondtoon en 1 of meer boventonen met een frequentie gelijk aan een heeltallig veelvoud van de grondtoon.
Bij de asymmetrische werklijn van fig. 2 onstaan er boventonen met frequenties 2, 3, 4, enz.. afhankelijk van de precieze vorm van de kromme werklijn.
Bij de symmetrische
werklijn van fig. 3 ontstaan er alleen oneven harmonischen.
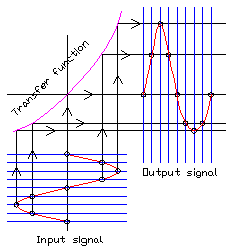
Fig 2. Kromme asymmetrische werklijn. Er is niet-lineaire vervorming. Er ontstaan even en meestal ook oneven harmonischen.
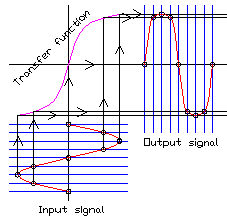
Fig 3. Kromme symmetrische werklijn. Er is niet-lineaire vervorming. Er ontstaan alleen oneven harmonischen.
Stel je bij de bovenstaande figuren eens voor dat het ingangs signaal bestaat uit de som van de getekende sinus plus nog een kleiner constant signaal van veel hogere frequentie. In de situatutie van fig. 1 komt dat hoogfrequente signaal onbeschadigd aan de uitgang. In fig. 2 en 3 varieert de versterking van dat hoogfrequentere signaal in het tempo van de laagfrequente sinus. Dit verschijnsel heet modulatie, en het resultaat is dat er som-en verschilfrequenties ontstaan van de oorspronkelijke componenten.
Als je op school ooit
goniometrie gehad hebt ben de je formule tegen gekomen voor het product van 2
sinussen of cosinussen met verschillende hoeken (frequentie)
Zo is 2 sin(a) * sin(b) = cos (a-b) - cos (a+b). Als je dus een sinus met
frequentie a moduleert (=vermenigvuldigt) met een sinus met frequentie b
ontstaan er frequenties (a+b) en (a-b).
Het muziek signaal is
een mengsel van allerlei verschillende frequenties. Als er ook nog som-en
verschil frequenties van al die bedoelde tonen bijkomen wordt het een flink
rommeltje. Intermodulatie vervoming dient dan ook onder de z.g. maskeringsgrens
te blijven. Dit betekent dat we een niet-lineare vervorming nastreven van minder
dan 0.1 % oftewel -60 dB of nog beter.
Er wordt in Hifi-land nog wel eens gediscussieerd over even- en oneven harmonischen, hoe die ontstaan en of ze mooi of lelijk klinken. Een groot deel van die discussie kan regelrecht de prullenbak in, als we even een klein uitstapje maken naar de muziektheorie, oftewel de harmonieleer.
Ik heb op het pianoklavier hieronder aangegeven waar de harmonischen van de toon c liggen. (c-klein = 130.81 Hz, bij de gelijkzwevende stemming op de kamertoon a' = 440.000 Hz)

Je ziet de even
harmonischen 2, 4 , 8 en 16 op de hele octaven liggen. Het octaaf geldt als het
meest welluidende interval of samenklank in de muziek.
De harmonischen 3, 6 en 12 liggen op de toon g. Het interval c-g heet een kwint,
en dat is na het octaaf het/de meest welluidende interval of samenklank in de
muziek.
De harmonischen 5, 10 en 20 liggen op de toon e. Het interval c-e heet een grote
terts, en die is na de kwint het meest welluidend.
De harmonischen 4, 5 en 6 vormen, als ze samen klinken het c-e-g accoord. Dit is
een z.g. "grote drieklank" en die geldt als het meest welluidende
accoord van 3 tonen.
Pas bij de 7e harmonische gaat het fout, die zit in de buurt van de bes2, maar wijkt zoveel af dat 'ie eigenlijk niet in de toonladder past.
De negende harmonische is een stapeling van 2 kwinten, die is ook niet helemaal zuiver maar het gaat nog net goed.
De 15e harmonische
ligt zo goed als op de b4. Het gelijktijdig laten klinken van twee naast elkaar
gelegen piano tonen klinkt meestal niet erg goed, maar we zitten hier hoog in de
diskant en dan kan het minder kwaad.
11, 13, 14, 17, en 19 passen echt niet in de (westerse) toonladders.
We zien dus dat zeker
tot-en-met de 8e harmonische alle boventonen en samenklanken daarvan gelden als
"zeer welluidend". Hoe kan iemand dan volhouden dat even harmonischen
lelijk zouden klinken en oneven mooi, of net andersom.
Ik denk dat de oorsprong van deze misvatting het volgende is: We moeten even
teug in de geschiedenis, naar de enkelvoudige klasse A buizenversterker. Deze
heeft een asymmetrische werklijn zoals in fig. 2,
en produceert daardoor flink wat vervorming waarvan de 2e harmonische veruit de
sterkste is. Als we deze versterker nu wijzigen in een (nog steeds klasse A)
balansversterker blijkt dat de tweede harmonischen van de twee eindbuizen elkaar
opheffen.
Bij andere symmetrisch opgebouwde versterkers, zoals ook bijna alle transistorverterkers geldt hetzelfde: Het gaat er niet om dat het een tweede of een andere even harmonische is, het gaat er om dat de tweede harmonische doorgaans de sterkste is en met een symmetrische opbouw van de versterker het gemakkelijkst te elimineren is.
Nog een opmerking over even en oneven harmonischen: Alhoewel de (symmetrie van de) werklijn er alles mee te maken heeft gaat het vooral om een eigenschap van Fourier-reeksen. Dat zijn optellingen van sinusen met heeltallige frequentie vehoudingen, zeg maar zuivere boventonen. Als er in zo'n reeks uitsluitend oneven boventonen voorkomen dan is de resulterende golfvorm altijd symmetrisch, ongeacht de amplitude en fase van die boventonen. Even boventonen maken de golfvorm altijd asymmetrisch. Daar is niets mis mee, maar voor deze discussie moet je het onderscheid kennen.
In de meeste eindversterkers wordt het vermogen voor de positieve helften van het signaal geleverd door het ene versterkings element (buis of transistor) en de negatieve helft door een soortgelijk ander element. Bij buizen versterkers worden die signaalhelften opgeteld met de uitgangstransformator, bij transistor versterkers worden steevast (quasi) complementaire transistors gebruikt.
In alle gevallen is het mogelijk dat het optellen van die signaalhelften niet helemaal goed gaat, waardoor er een uitgangssignaal ontstaat zoals hieronder getekend.
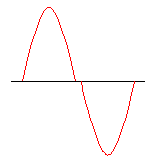
Fig 5. Signaal met overneem vervorming. (eng: cross-over distortion)
Dit is een heel vervelende soort vervorming, vooral omdat de ernst ervan toeneemt naarmate je bij een lager geluidsvolume luistert. In een extreem geval kan het gebeuren dat je beneden een bepaald volume helemaal niets meer hoort.
Het is vrij gemakkelijk om je apparatuur te testen op dit soort vervorming. Draai op een stille avond wat rustige muziek en zet het volume steeds zwakker. Verwijder zonodig het front-doekje van je kasten en luister met het oor aan de luidsprekers of het nog zuiver klinkt. Als het geluid schor of krakerig gaat klinken bij een laag volume is het beslist fout, en moet je je versterker(s) laten nazien. Maar let op! een defecte luidspreker, of als er rommel (ijzervijlsel!) tussen de spreekspoel en de magneetpool is gekomen kan hetzelfde soort vervorming opleveren. Dus test ook nog even met een onverdachte versterker en/of onverdachte luidsprekers.
Dit treedt op wanneer je de (eind) versterker overstuurt. De versterker is simpelweg niet in staat meer uitgangs signaal te leveren.
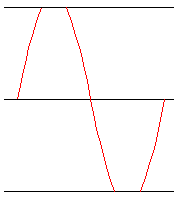
Fig. 6. Typisch geval van clipping.
Het gebeurt nog al eens dat er bij de overgang van normaal bedrijf naar clipping -en andersom- hoogfrequente oscillaties plaatsvinden. Dit is sterk afhankelijk van de constructie van de versterker.
Hoewel diverse versterker ontwerpen nogal verschillen in het gedrag bij oversturing is dat voor huiskamer hifi weergave tamelijk oninteressant. Je mag je versterker nu eenmaal niet oversturen.
In bewerking
Dit is een type vervorming dat alleen bij luidsprekers optreedt.
We
kennen het Doppler Effect vooral van de voorbijrijdende politie- brandweer- of
amulance auto met sirene. Als de auto komt aanrijden worden de geluidsgolven
a.h.w. in elkaar gedrukt en lijkt de toon hoger; als de auto van je af rijdt
worden de geluidsgolven "uitgerekt" en wordt de waargenomen toon
lager.
Dit zelfde effect kan ook optreden in luidsprekers, in het bijzonder bij
luidsprekers die de zeer lage frequenties moeten weergeven en ook nog vrij veel
hogere tonen doen. Bedenk dat de conus uitslag bij basluidsprekers meestal
aanzienlijk is. De "bron" voor de midden tonen beweegt dan heen-en
weer in het tempo van de bas.
Er treedt zodoende een frequentie modulatie op die leidt tot vervorming of
vertroebeling op van de hogere tonen. Dit is 1 van de redenen om verschillende
luidsprekers (chassis) te gebruiken voor de verschillende frequentie gebieden.
Een reken voorbeeldje: Een basluidspreker geeft een toon van 30 Hz weer, met een conus uitslag van 1 cm piek-piek. Stel dat die luidspreker ook een toon van 1 kHz moet weergeven. Geluid van 1 kHz heeft een golflengte van zo'n 30 cm. We hebben dan een bron die een 30 cm lange golf moet produceren, terwijl 'ie zelf al 1 cm heen-en-weer gaat. Je moet hier een vervorming van meer dan 1 procent verwachten.
Voor de wiskundigen: deze vervorming laat zich beschrijven met de formules voor de zijbanden en harmonischen bij Frequentie Modulatie.
Dit type vervorming neemt toe met de geluidssterkte waarop je speelt. Kleine luidsprekerkasten zijn hier in het nadeel omdat daar relatief kleine basluidsprekers gebruikt worden waarbij de conus een grote uitslag moet maken om een bepaald geluidsnivo te halen (baspomp) . Nog erger wordt het als het ook een tweeweg-systeem is met een hoge scheidings frequentie.
De snelheid van de conus is in dit voorbeeld 2 * pi * 30 / 100 = 1.8 m/sec of bijna 7 km/uur. Dat is niet erg snel voor een ambulance, maar als 'ie met die snelheid voorbij komt dan zakt de sirenetoon toch wel een halve toets op de piano.
.